Sifat

1.Kalor dapat mengubah suhu suatu benda

Benjamin Thompson yaitu ilmuwan asal Amerika tahun 1798 melakukan pengamatan dari 2 suhu yang dicampur menjadi 1 dan diberikan kesimpulan bahwa: jumlah kalor yang diperlukan untuk mengubah suhu suatu benda ditentukan oleh massa suatu zat (m), perubahan suhunya (Δt), dan kalor jenis zat (c) benda yang dipanaskan

Sehingga dapat dirumuskan:

Q= m x c x Δt

Ket:

Q = Jumlah kalor yang diperlukan unutk mengubah suhu suatu benda (joule) 

m = Massa benda (kg)

c = Kalor Jenis Zat (joule/kg °C)

Δt = perubahan suhu (°C)/ selisih suhu yaitu t₂ - t₁

Kalor jenis suatu zat adalah banyaknya kalor yang diperlukan untuk menaikkan suhu 1kg zat sebesar 1°C atau 1K

Kalor Jenis berbagai Zat

 

Zat	Kalor Jenis (J/Kg°C)
Udara	1000
Air	4200
Alkohol	2400
Raksa	140
Parafin	2200
Es	2100
Aluminium	900
Tembaga	390
Kaca	670
Besi	450
Emas	130
Perak	234

Ket: Semakin rendah kalor jenis suatu benda maka akan lebih cepat panas

Kalorimeter adalah alat untuk mengukur kalor.

Salah satu bentuknya adalah kalorimeter campuran

 

Pengaruh Kalor dalam kehidupan sehari - hari: pada daerah pantai

Kapasitas kalor: Jumlah kalor yang diperlukan untuk menaikkan suhu 1°C atau 1K

Dirumuskan:

Q = C x Δt

C = m x c

Ket:

Q = jumlah kalor (joule)

C = Kapasitas kalor (J/°C atau J/K)

m = Massa benda (kg)

c = Kalor jenis zat (joule/kg °C)

Δt = Perubahan suhu (°C)  2. Kalor dapat mengubah wujud suatu benda 

 
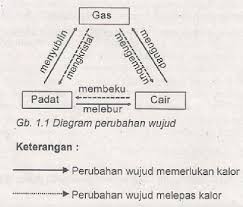
Perbedaan mendidih dan menguap:
Mendidih : 100 °C, seluruh permukaan, terdapat gelembung udara
Menguap : dibawah 100 °C, permukaan tidak ada gelembung udara  

Menyerap kalor : endoterm
Melepas kalor : eksoterm 
Deposisi : perubahan wujud benda dari gas ke padat tanpa ada fase cair

Banyaknya kalor yang diserap atau yang dilepaskan (Q) dalam proses perubahan wujud benda dapat dinyatakan dengan rumus:

Q = m x L

Ket:

Q = Jumlah kalor (joule)

m = Massa benda (kg)

L = Kalor laten (Kalor lebur, kalor beku, kalor uap, kalor embun, kalor sublim, kalor kristal)(J/kg)

Kalor laten adalah kalor yang diserap atau yang dilepas pada saat terjadi perubahan wujud benda tidak menyebabkan perubahan suhu benda (suhu benda konstan)

Kalor laten beberapa zat

Kalor uap = kalor embun
Kalor didih = titik embun